Desvendando la regresión lineal

No importa si eres nuevo o tienes más experiencia en el mundo de los datos, pero es muy probable que hayas oído hablar de la famosa regresión lineal o hayas ajustado una línea para visualizar la relación entre dos fenómenos. Pero, entre nosotros, ¿cómo funciona este algoritmo? O incluso, ¿qué ocurre detrás de la predicción de datos cuando utilizamos esta técnica?

La regresión lineal simple es una metodología que estudia la relación entre dos fenómenos, lo que nos permite comprender el efecto y la causalidad entre ellos, así como predecir nuevos valores. Para entenderlo mejor, vamos a desvendar cómo ajustar la línea, interpretar y predecir los valores.

Ajuste de la recta

La relación entre dos factores se estudia mediante regresión lineal simple utilizando una fórmula que dibuja una línea. Para entender mejor esta relación, utilizaremos uno de los estudios del economista John Keynes. Concluyó que los individuos tienden a aumentar su consumo a medida que aumentan sus ingresos.

En la siguiente tabla, podemos ver las primeras cinco observaciones del conjunto de datos que utilizaremos:

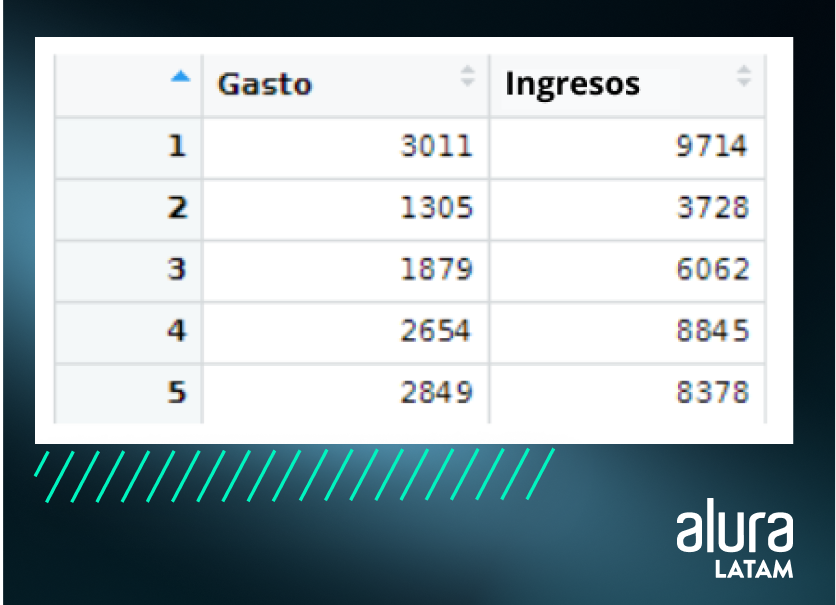
Podemos crear una relación entre gastos e ingresos de la siguiente manera:

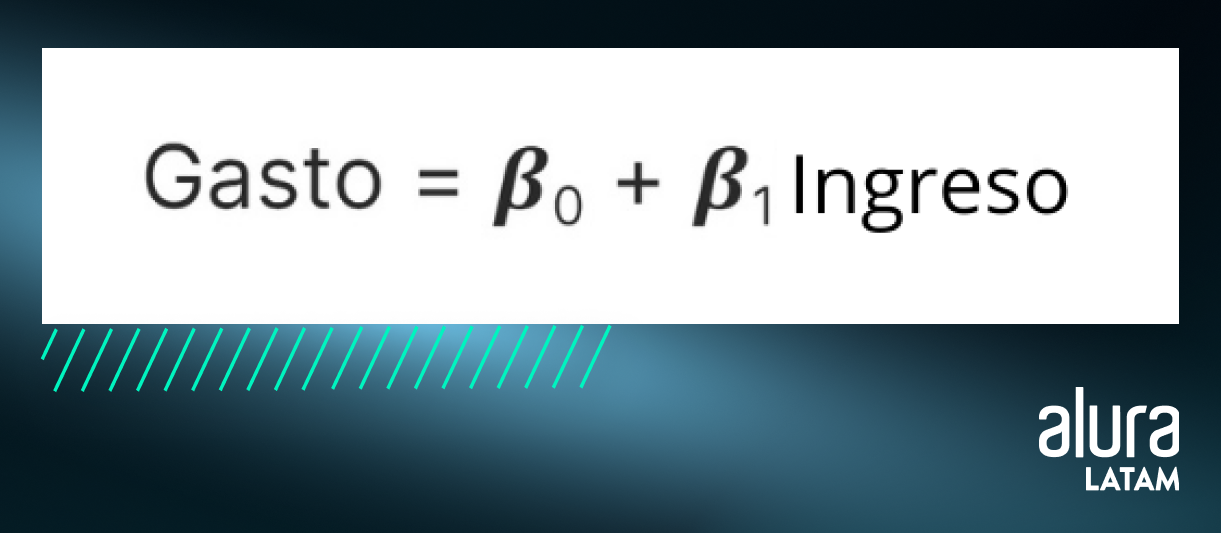
Aquí, cada componente representa un conjunto de valores, siendo:

• Gasto: gasto o consumo del hogar
• Ingreso: ingreso disponible
• β0: consumo cuando el rendimiento es cero
• β1: propensión marginal a consumir

Usando el conjunto de datos como ejemplo, esta función dibuja la siguiente línea:Gasto = 207.9 + 0.3Ingreso + erro

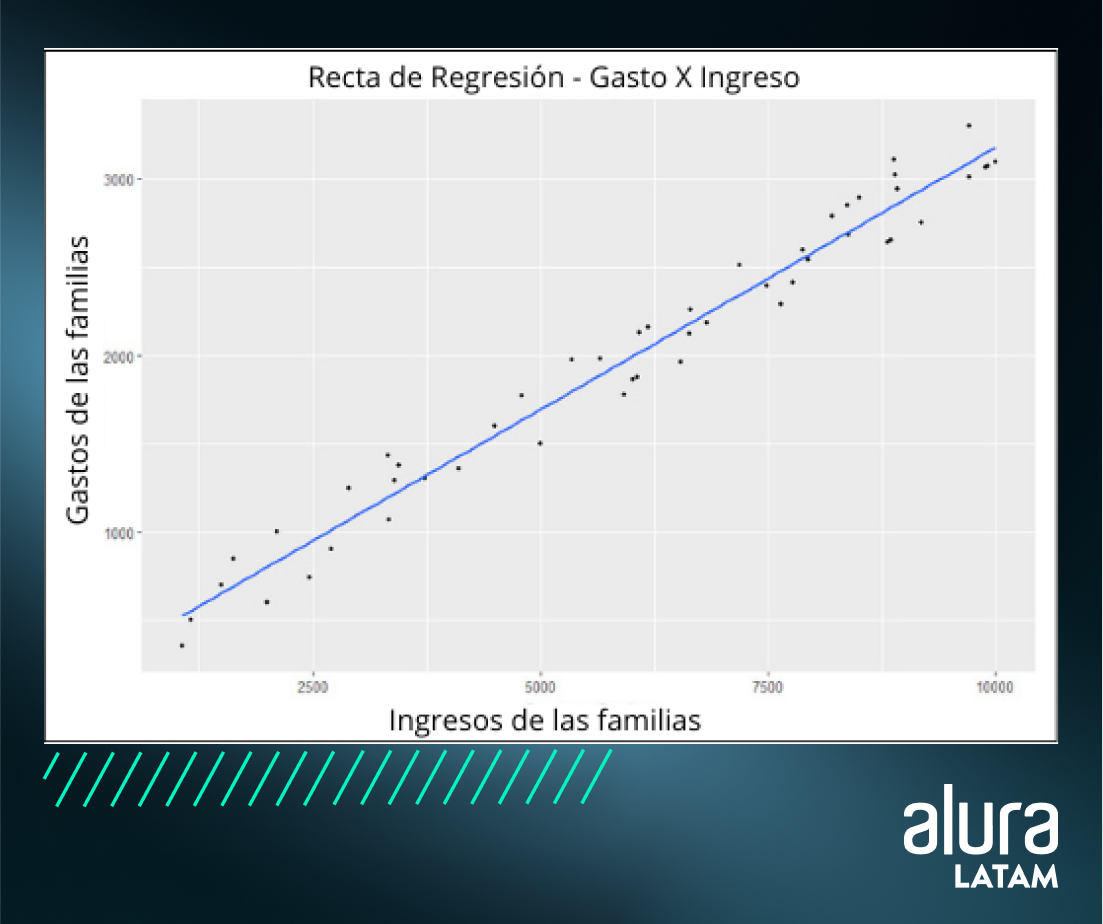
Podemos ver que cuanto menor es el ingreso (X), menor es el gasto de las familias (Y). En el centro, hay una nube de puntos en la que se ha ajustado una línea lineal en forma de media luna que permite entender el comportamiento medio del gasto de los hogares. Pero, ¿cómo pasamos de la función a ? Gasto = 𝜷0+ 𝜷1Ingreso + erro``Gasto = 207.9 + 0.3Ingreso + erro

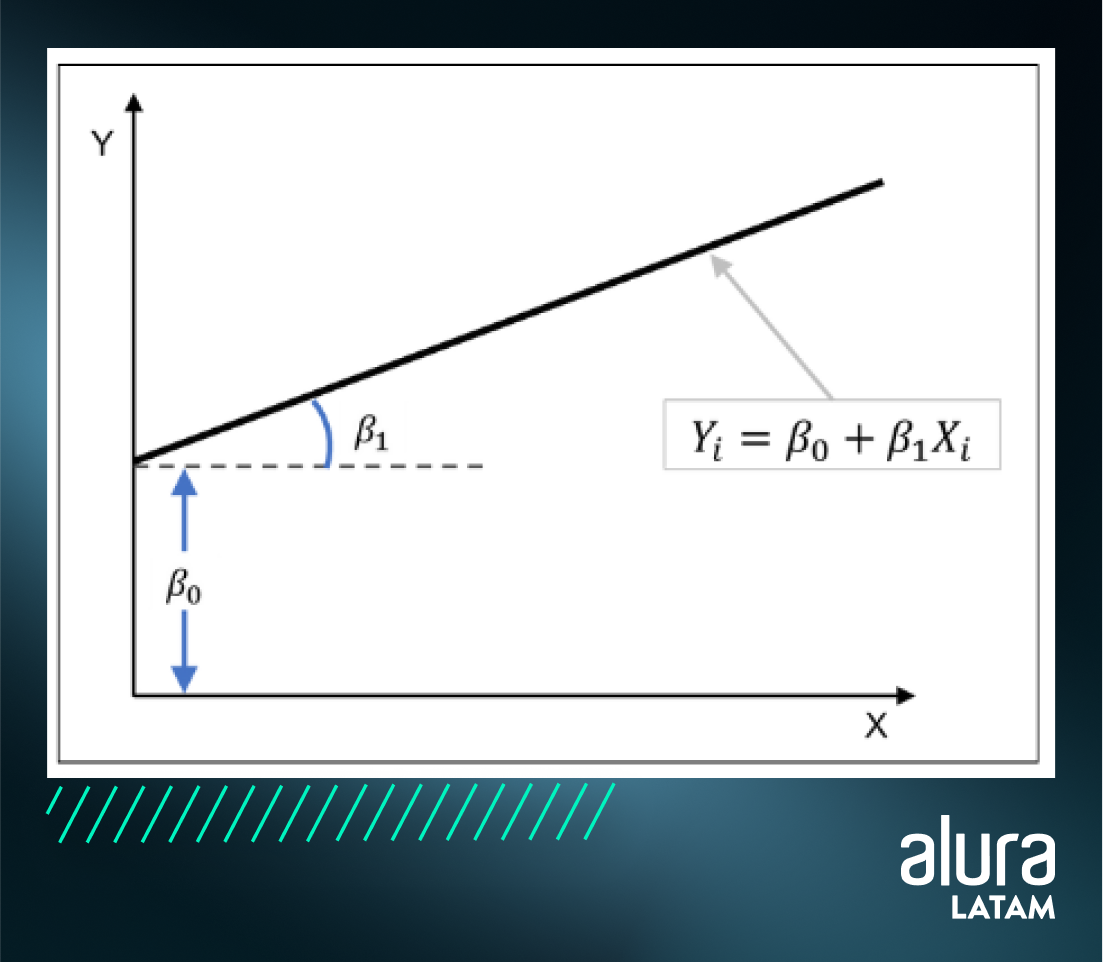
Independientemente de su conjunto de datos, se ajustará una línea que podemos representar genéricamente mediante la siguiente función:

Y es el conjunto de valores que depende de una explicación y X es la variable independiente y explicativa. En nuestro ejemplo, el gasto de la familia depende de sus ingresos. El β0, también llamado intersección, es el valor de Y cuando Xi es cero. Por otro lado, β1, la pendiente, nos dice la tasa de cambio y qué tan empinada será nuestra línea.

Ambos parámetros, β0 y β1, son desconocidos y necesitan ser estimados. Aquí no nos extenderemos sobre este tema, pero sabemos que uno de los procesos más utilizados para estimar estos coeficientes es el método de mínimos cuadrados. En resumen, este método crea una línea lo más cercana posible a los valores disponibles en la que la diferencia entre el valor real de Y y el valor esperado es mínima.

A partir de nuestros datos y de este proceso de estimación, podemos calcular las betas con las siguientes fórmulas:

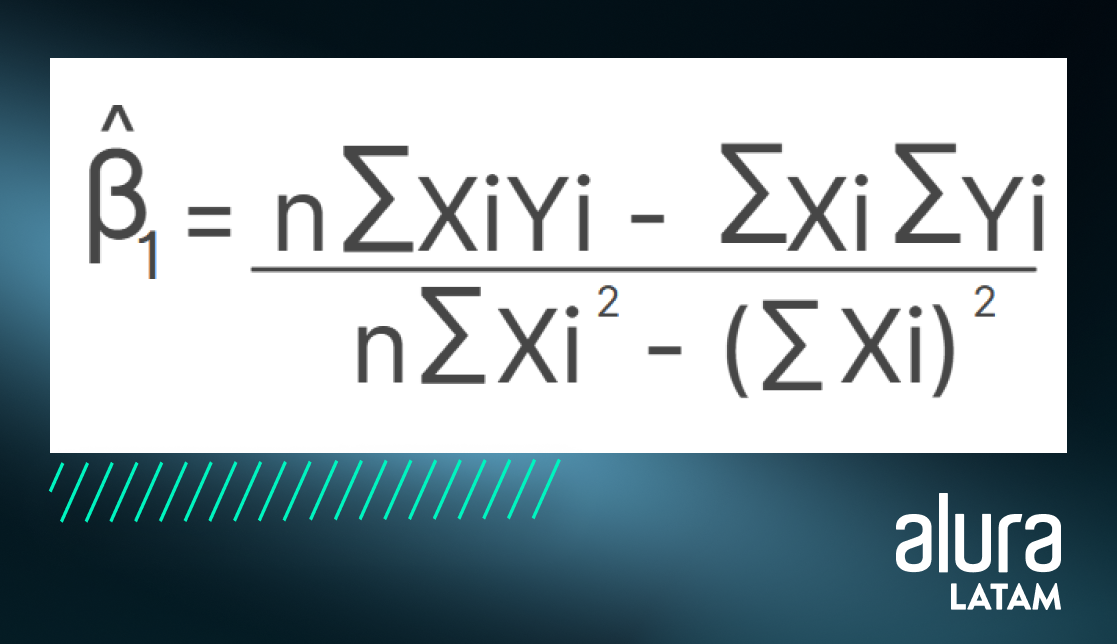
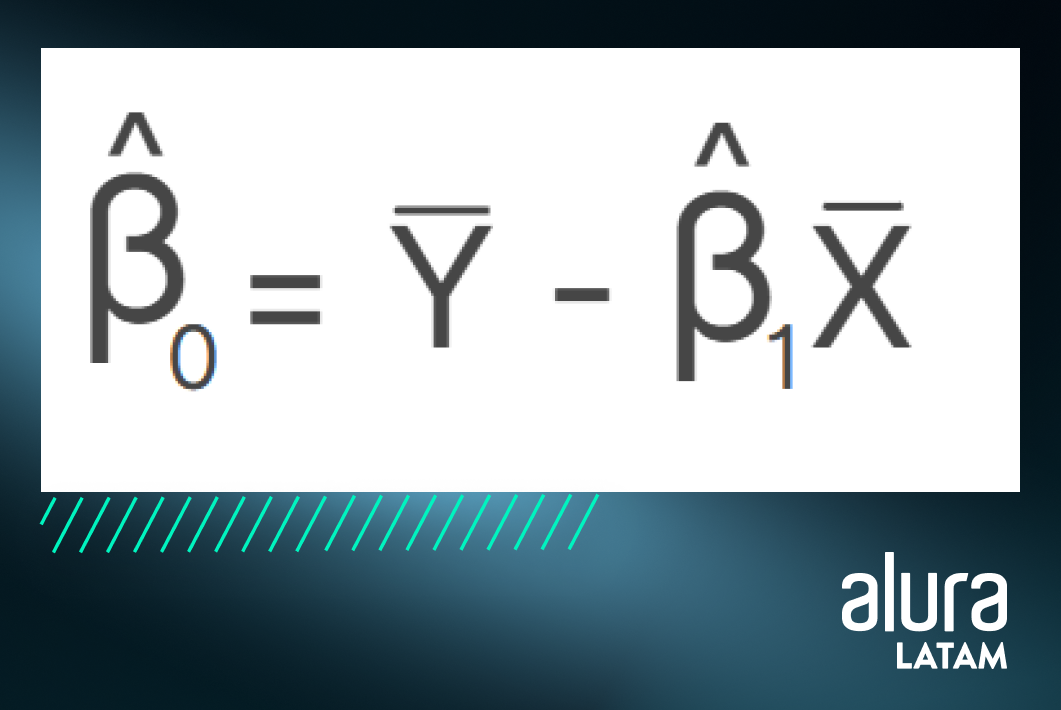
Formando:

Gasto =  207.9 + 0.3Ingreso + erro

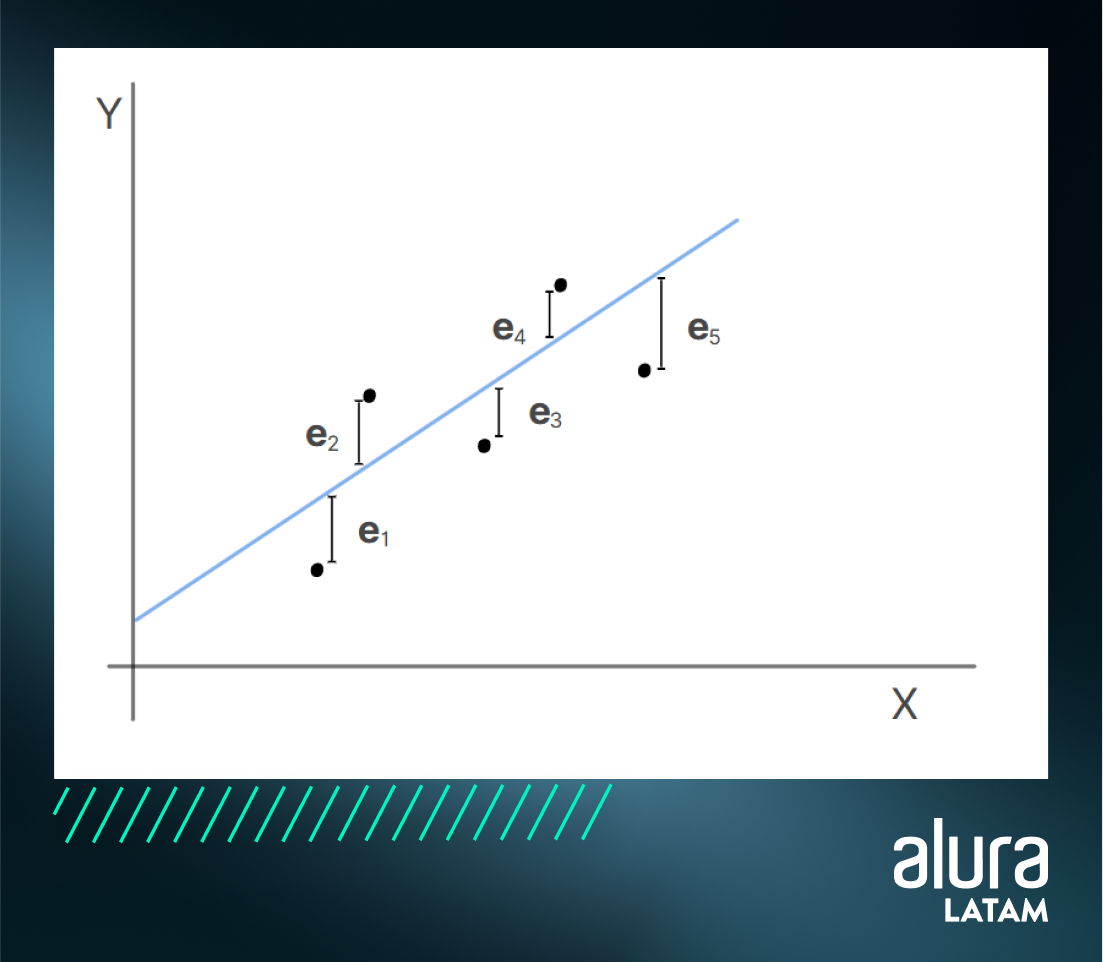
Es posible que haya notado que no todos los puntos están alineados en la línea que ajustamos. Para hacer esto, necesitamos agregar el error a nuestra fórmula, que es precisamente la diferencia entre el valor observado y el valor proporcionado por la ecuación.

Ahora que conoces mejor todos los miembros de la regresión lineal, es importante que sepas que la variable de respuesta (la que estamos tratando de explicar y que depende de otros factores), debe ser cuantitativa, es decir, debe tener valores numéricos.

En nuestro caso, la variable de respuesta es el gasto familiar. Otros ejemplos de variables son:

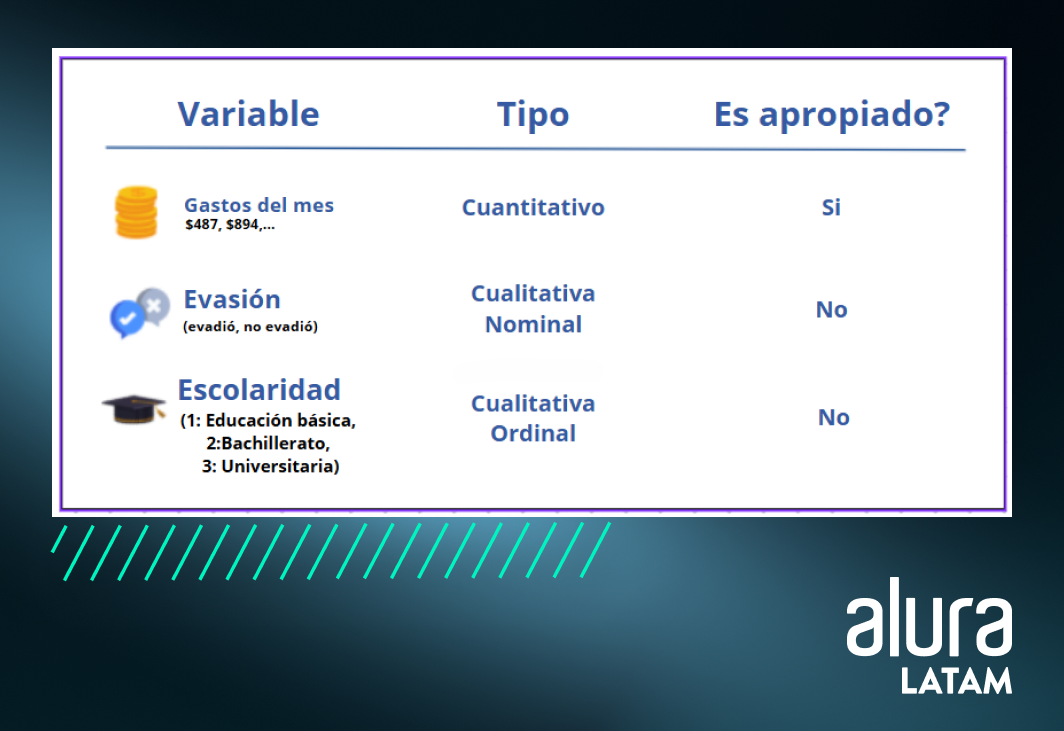
Si lo que se busca estudiar no está dispuesto en valores numéricos, capaces de tomar promedios y otras métricas, la regresión lineal no es el método más adecuado. En este caso, puede utilizar otras metodologías, como la regresión logística o los métodos de clasificación.

Interpretación de los valores

Ya has ajustado la línea y además conoces a cada uno de los miembros de nuestra función. Volvamos al ejemplo y entendamos qué significa cada valor en la práctica.

Pasamos de

Gasto = 𝜷0 + 𝜷1Ingreso + e

a esto

Gasto =  207.9 + 0.3Ingreso + e

En nuestro caso, β0 es 207,9, es decir, el consumo (cuando no hay ingresos) es 207,90 reales. El coeficiente relacionado con los ingresos (β1) indica que, por cada real adicional en ingresos, el gasto promedio esperado aumenta, en promedio, 0,30 reales. De esta manera, se cuantifica el efecto de los ingresos sobre el gasto.

Predicción de valores

Imagina que una familia tiene un ingreso de 3 mil reales, ¿cuánto sería el gasto estimado según nuestro modelo? Podemos sustituir 3.000 en la fórmula y obtener un gasto esperado estimado de .Gasto = 207,9 + 0,3*(3000) = 1107,9

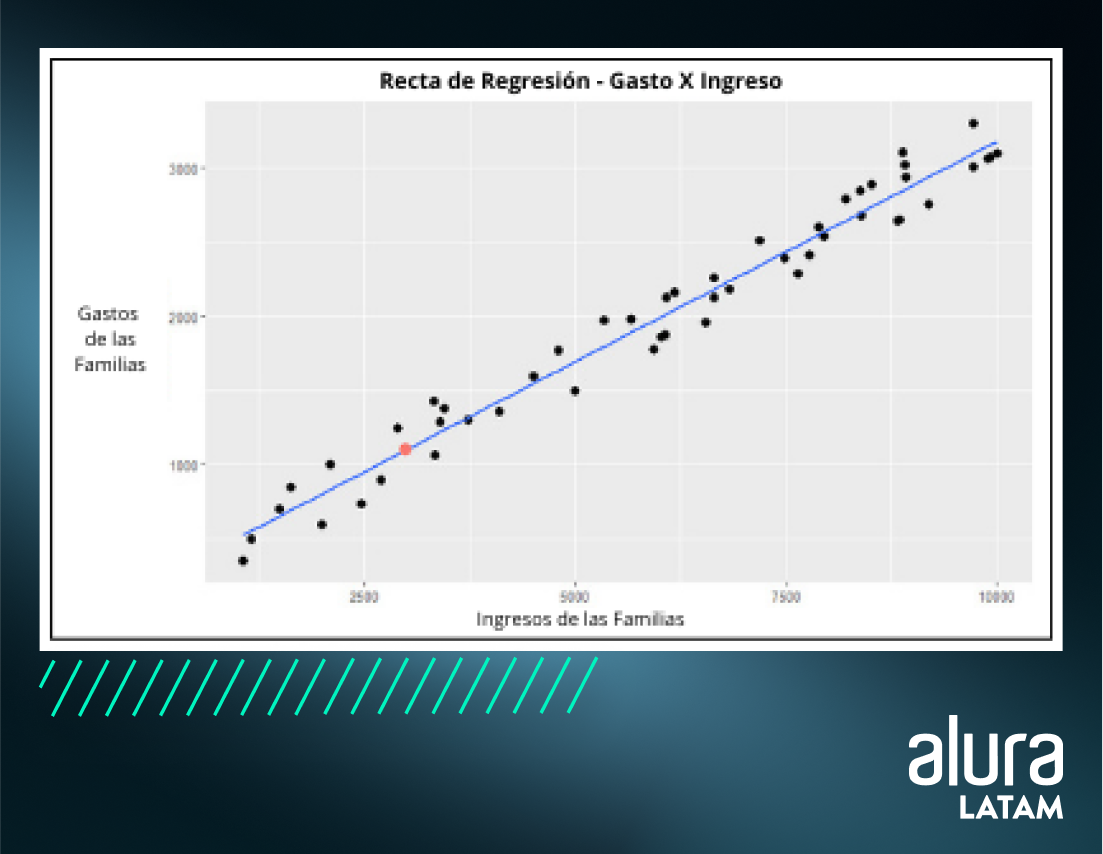
El punto rosa en el gráfico muestra nuestro valor previsto basado en los ingresos de tres mil reales de ingresos familiares. Hay que tener en cuenta que la línea de regresión es capaz de cuantificar la relación entre las variables explicativas y la respuesta y de predecir un nuevo valor.

Hay otros detalles de la teoría, pero, en general, la regresión lineal es una metodología que estudia la relación entre dos fenómenos. A través de una fórmula, es posible comprender el efecto que tiene la variable explicativa sobre la variable de respuesta, además de hacer predicciones de nuevos valores.

Puedes profundizar tus conocimientos con el curso Regresión Lineal aquí en Alura Latam.

Ana Duarte

Soy licenciado en Estadística y actualmente estoy estudiando Ciencias de la Computación. He trabajado como científica de datos en el ámbito educativo y financiero y hoy soy instructora en la escuela de Datos de Alura y voluntaria en el equipo de proyectos del grupo Data Girls. Me apasiona transformar los datos en información inteligente utilizando la ciencia de datos en diversos tipos de aplicaciones. Aparte de eso, siempre estoy siguiendo alguna serie y buscando nuevas rutas para andar en bicicleta.

Artículo adaptado y traducido por Daysibel Cotiz.