¿Qué son los algoritmos de clustering y cuándo utilizarlos?

Estos grupos también se conocen como clústeres , por lo que el análisis de clústeres también puede llamarse agrupamiento .

Con esto en mente, en este artículo exploraremos los principales algoritmos de clusterización, sus diferencias y cuándo utilizarlos. Para ello, revisaremos los siguientes algoritmos:

• K-medias
• DBSCAN
• Mean Shift
• y finalmente, la técnica de Clusterizaçion jerárquico

¿Vamos?

Cómo funciona la técnica de agrupamiento

El primer punto importante es que una de las principales ventajas de las técnicas de clusterización es etiquetar los datos con la información que queremos predecir. Es decir, el análisis es de naturaleza exploratoria .

Existen numerosas técnicas y criterios diferentes para definir la similitud entre datos y formar grupos.

Estas técnicas se utilizan en una amplia gama de áreas, como sistemas de recomendación, segmentación de clientes y detección de anomalías.

Los criterios de similitud y disimilitud de estas técnicas generalmente implican el cálculo de la distancia entre registros en la base de datos. Por lo tanto, solo se puede utilizar información binaria (0 o 1) o numérica en la evaluación de similitud.

Además, debido a los cálculos de distancia, estos algoritmos son muy sensibles a la presencia de valores atípicos y a la diferencia de escala entre las variables en la base de datos.

Dicho esto, exploremos nuestro primer algoritmo que es K-Means.

K-medias

El algoritmo K-Means es uno de los algoritmos de agrupamiento más populares y su tarea es dividir un conjunto de datos en k grupos distintos.

El objetivo de este algoritmo es minimizar la varianza de los datos dentro de cada clúster. En otras palabras, el objetivo es maximizar la similitud entre los puntos dentro de un clúster y maximizar la divergencia de características entre diferentes clústeres.

El algoritmo K-Means funciona básicamente de la siguiente manera:

• Se define un número inicial de clústeres en los que se dividirán los datos y se delimita la posición de los centroides. Los centroides son puntos que representan un grupo, generalmente en la posición central de los puntos.
• El algoritmo calcula la distancia de cada punto a cada centroide y asigna al punto un grupo que hace referencia al centroide más cercano.
• Después de definir los grupos iniciales, cada centroide se reposiciona en la posición promedio de los puntos en cada grupo.
• Los dos pasos anteriores se repiten hasta que no haya variación en la posición de cada clúster y en la asignación de grupo de cada punto.

La siguiente visualización representa el proceso iterativo de K-Means con 3 clusters, con la definición de la posición de los centroides iniciales y su reposicionamiento en función del punto medio de los puntos:

Cuándo utilizar K-Means

• Cuando se tiene un conjunto de datos grande y se conoce o se puede estimar el número de clústeres k.
• Cuando buscamos una solución rápida y eficiente para agrupar datos.
• Cuando la distribución de datos es aproximadamente esférica, dado que el cálculo de la distancia se realiza desde un centro a cada punto, los grupos formados generalmente tendrán una forma esférica/circular.

DBSCAN

DBSCAN es un algoritmo de agrupamiento que se basa en la densidad de puntos.

Esta técnica agrupa los puntos cercanos entre sí en grupos e ignora las regiones donde la densidad de puntos es baja, es decir, cuando los puntos están muy espaciados.

Es capaz de identificar clusters de forma arbitraria, sin necesidad de definir previamente el número de grupos a formar y se ve poco afectado por la presencia de valores atípicos.

Para que el algoritmo DBSCAN funcione es necesario definir un valor de épsilon (ε) que determina la distancia máxima a considerar para agrupar dos puntos en un mismo cluster.

Otro parámetro a definir es el número mínimo de puntos dentro de un vecindario para que se pueda definir el cluster.

El proceso de generación de clusters mediante el algoritmo funciona de la siguiente manera:

• Se selecciona aleatoriamente un punto de la base de datos.
• El cálculo de la distancia de una esfera con radio épsilon (ε) se realiza alrededor del punto seleccionado.
• Si se estipula inicialmente un número mínimo de puntos dentro de la esfera, estos formarán parte de un grupo. De lo contrario, el punto se considerará ruido.
• El proceso se repite para los puntos asignados al clúster hasta que la condición deje de cumplirse. En ese caso, se elige aleatoriamente un nuevo punto para definir un nuevo clúster o ruido.

La siguiente visualización representa el proceso iterativo de DBSCAN. En cada punto, se forma un círculo de tamaño épsilon (ε) y se comprueba si hay al menos 3 puntos en esta vecindad. De ser así, los puntos se asignan a un clúster:

Cuándo utilizar DBSCAN:

• Cuando los cúmulos tienen formas complejas, distintas de las esféricas.
• Cuando los datos contienen ruido y valores atípicos.
• Cuando no es posible definir el número de grupos que formará el algoritmo.

Mean Shift

Mean Shift es un algoritmo que se basa en centroides, al igual que K-Means. Sin embargo, encontrará automáticamente el número de clústeres, por lo que no es necesario definir este número de antemano.

Se basa en la idea de encontrar máximos locales en la densidad de puntos para descubrir los centros de los cúmulos.

Funciona actualizando los candidatos a centroide para que sean el promedio de los puntos dentro de una región determinada.

Los candidatos a centroide se filtran para eliminar puntos duplicados o puntos que están demasiado cerca entre sí, formando así un conjunto final de centroides.

El tamaño de la región a buscar está determinado por un parámetro bandwidth o ancho de banda, y puede definirse de forma manual o automática en función de una estimación.

La siguiente visualización representa el proceso iterativo del Desplazamiento Medio. Primero, se asignan diferentes centroides posibles y, basándose en el cálculo para obtener un valor máximo, conocido como "hill climbing" , los centroides se reasignan cada vez más cerca del valor máximo de densidad hasta definir el centro de un clúster:

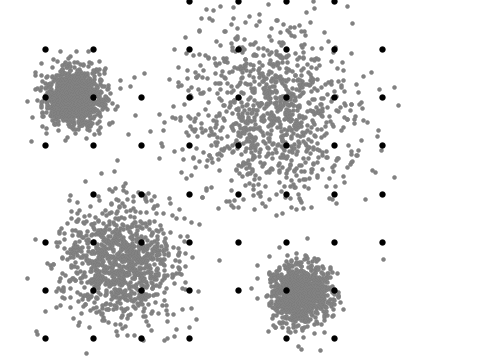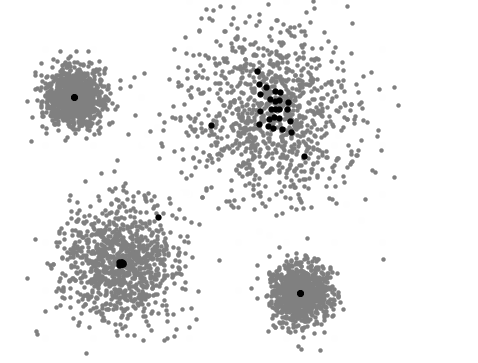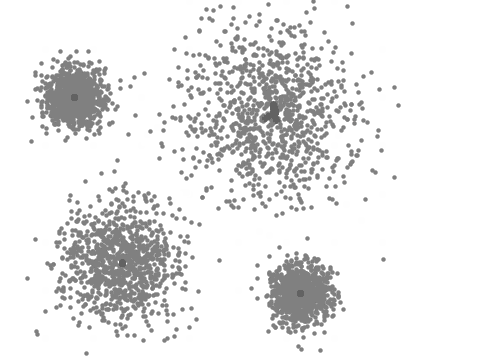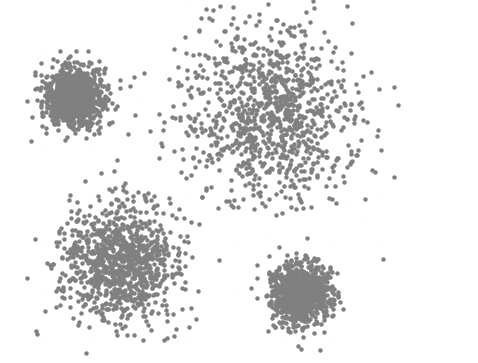
Cuándo utilizar Mean Shift:

• Cuando no es posible definir el número de grupos que formará el algoritmo.
• Cuando los clústeres tienen formas y tamaños arbitrarios.
• Cuando la base de datos no tiene muchas filas o variables, el algoritmo de desplazamiento medio es muy costoso computacionalmente y, al trabajar con muchas variables, puede no converger bien en las iteraciones.

Clusterización jerárquico

La clusteriazación jerárquica es una técnica muy eficiente para determinar la cantidad de clústeres y tener una visión general de cómo se agrupan los datos.

Cada una de las observaciones comienza en su propio grupo y luego los grupos se fusionan sucesivamente en función de la similitud de los datos.

Esta similitud se calcula a partir de una métrica de distancia, como la euclidiana.

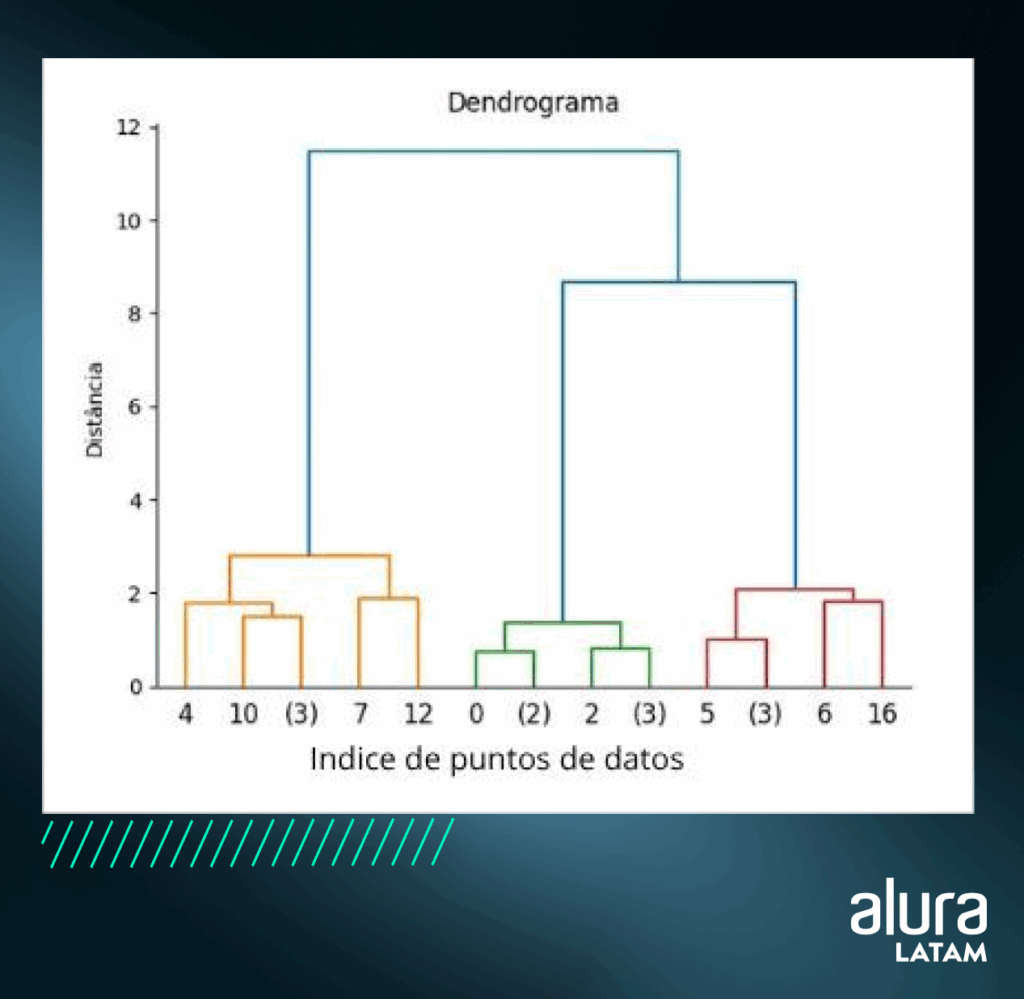
Al final de todo el proceso de iteración, este algoritmo produce una visualización jerárquica de grupos en forma de árbol, denominada dendrograma.

A partir del dendrograma, es posible identificar qué datos son más similares entre sí y el número de clusters en que se dividirán los datos.

La imagen de abajo es una representación de un dendrograma, en el que los datos se dividieron en 3 grupos, en los colores naranja, verde y rojo.

El eje y representa la distancia de un registro a otro, lo que significa que los puntos más cercanos están en el mismo grupo y los puntos más distantes están en grupos diferentes:

Cuándo utilizar la clusterización jerárquica:

• Cuando desee visualizar la estructura jerárquica de los datos.
• Cuando no se conoce el número ideal de clusters.
• Cuando los clústeres tienen formas y tamaños arbitrarios.

Conclusión

En este artículo, fue posible comprobar los siguientes algoritmos de clustering, sus diferencias y cuándo podemos utilizarlos:

• K-medias
• DBSCAN
• Cambio medio
• y la técnica de clusterizacion jerárquico

Es importante tener en cuenta que cada algoritmo tiene sus propias ventajas y limitaciones, y la elección del algoritmo correcto depende de la naturaleza de los datos y los objetivos del análisis.

Por último, si quieres profundizar aún más en el contenido de este artículo, te sugiero nuestra Formación en Machine Learning , donde un equipo de expertos te ayudará a avanzar aún más en tu carrera y te permitirá adquirir cada vez más conocimientos en el área.

Un abrazo y hasta luego.

Referencias

• Documentación oficial de scikit-Learn: Sección de agrupamiento
• Libro: Manual de análisis de datos
• Artículo: Agrupamiento con Scikit y GIF

Créditos
Creación textual: Juan Víctor de Miranda
Articulo adaptado y traducido por Daysibel Cotiz.